TUGAS MANDIRI MATRMATIKA DISKRIT KAMPUS MILENIAL ITBI MEDAN

Tugas mandiri Matematika Diskrit

Nama:yusni Sari Sipahutar

Jurusan:Tehnik Informatika

Kelas;Pagi

Soal;

1》Buatlah 3 contoh soal dan penyelesaian tabel kebenaran 

Jawab;

1 Tunjukkan bahwa p→q ekivalen secara logika dengan ~p q.

Penyelesaian :

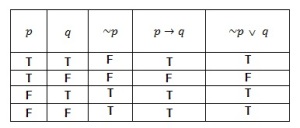
Tabel 1.9 memperlihatkan bahwa memang benar p→q~p  v q. Dengan kata lain pernyataan “Jika p, maka q” ekivalen secara logika dengan “ tidak p atau q”.

Tabel 1.9 tabel kebenaran p→q dan ~p v q

Tentukan ingkaran (negasi) dari p→q

Penyelesaian :

Dari contoh 1.15 sudah ditunjukan bahwa p→q ekivalen secara logika dengan ~p q gunakan hukum DeMorgan untuk menentukan ingkaran dari p→q :

~(p→q) ~(~p q)   ~(~p)~q  p~q

 

Dua pedagang barang kelontong mengeluarkan moto jitu untuk menarik pembeli. Pedagang pertama mengumbar moto “Barang bagus tidak murah” sedangkan pedagang kedua mempunyai moto “Barang murah tidak bagus”. Apakah kedua moto tersebut menyatakan hal yang sama ?

Penyelesaian :

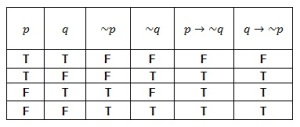
Untuk memeriksa “Apakah kedua moto tersebut sama, kita perlu membandingkan tabel kebenaran keduanya. Misalkan p menyatakan proposisi “Barang itu bagus” sedangkan q menyatakan “Barang itu murah”. Maka moto pedaganf pertama dapat ditulis sebagain “Jika barang itu bagus maka barang itu tidak murah” atau p→~q, sedangkan moto kedua dapat ditulis sebagai “Jika barang itu murah maka barang itu tidak bagus” atau q→~p. Tabel kebenaran untuk proposisis p→~q dan proposisi q→~p sama, dengan kata lain p→~q q→~p. Jadi kita dapat menyimpulkkan bahwa kedua moto tersebut menyatakan hal yang sama.

Tabel 1.10 tabel kebenaran p→~q dan q→~p

Banyak orang yang bingung mengapa bentuk “p hanya jika q” sama dengan “jika p, maka q” untuk menjelas hal-hal ini kita harus mengingat bahwa “p hanya jika q” menyatakan bahwa p tidak dapat benar bila q salah. Dengan kata lain, menyatakan “p hanya jika q” salah jika p benar, tetapi q salah. Bila p salah, q dapat salah satu dari benar atau salah, karena pernyataan tersebut tidak menyatakan apa-apa tentang nilai kebenaran q .

2》jelaskan konsep dari matematika graf yang sudah di pelajari

Dalam matematika dan ilmu komputer, sebuah graf adalah objek dasar pelajaran dalam teori graf. Dalam bahasa sehari-hari, sebuah graf adalah himpunan dari objek-objek yang dinamakan titik, simpul, atau sudut dihubungkan oleh penghubung yang dinamakan garis atau sisi.